Fitting Regression Model and Optimization of Cutting Parameters In Order To Achieve Economical Machining Of a Cryogenic Soaked Magnesium Alloy

Abstract

In present times many industries are giving more importance in reducing the overall cost of production and in this regard reduction in weight of the work material has become necessary which in turn reduces the power consumption required for machining and hence leads to reduction in overall costs. Thus usage of light weight materials has garnered deep interest in the industries. This project deals with the turning of Mg AZ31B alloy for the above stated reasons. The objective of this work is to optimize the influencing cutting parameters like speed, feed, depth of cut and approach angle of the cutting tool by using experimental engineering design techniques like Taguchi method of orthogonal array, analysis of variance method to compute contribution of each of these parameters on the quality of machined output. The response variables taken up for this analysis were surface roughness, material removal rate, tool wear rate and machining time as all these factors governs the quality of the machined product and hence relates to economics of machining. Regression models have been developed in order to study about the mathematical relation between the input cutting parameters and each of the output variables. Contour plots have been drawn to study about interactions between the input cutting parameters and its impact on the output variables. In order to study the effect of cryogenic soaking on the work specimen Vickers hardness test has been performed to check the enhancement of the hardness before and after cryogenic soaking. The experimental data shows that surface roughness is mostly affected by approach angle of the cutting tool whereas material removal rate, tool wear rate and machining time were mostly affected by depth of cut. From the confirmatory test it was evident that Taguchi analysis helps in optimizing the output variables. It was also observed that cryogenic soaking suitably increases the hardness of the material thus making it more machinable.

Introduction

I. INTRODUCTION

The ultimate aim of a production engineer is to produce a product which is economical in terms of overall cost of production. Among all the manufacturing processes available between us it is being observed that metal removal processes are the most expansive ones. It is primarily due to the fact it requires more amount of energy to perform the intended function of removing excess material from the work metal in form of chips to obtain the desired shape and size of the final product. Among all the various kind of machining process available which can be performed in a lathe machine, turning is the most prominent of them. The primary goal of a turning operation is to reduce the diameter of the workpiece to the appropriate size. The ultimate requirement with regard to any of the available machining operation is that it should result into lowest possible unit cost and highest possible production rate. In any of the manufacturing operation, the cost involved plays an important role in determining how much should be the rate of production. This motive of attaining economical machining is achieved by analysing the machining process and identifying critical cutting parameters which has definite influence on the machining operation so that it can be optimized which will eventually leads to obtain an economical machining output. Thus identification of critical of parameters plays a paramount role. Among the many available light weight materials, aluminium alloys are vastly used in various industrial applications. From its utility in coke canes to aircraft fuselage, aluminium alloys due to its cheaper cost, ease of fabrication and lighter weight enjoys most popularity among the other materials.

But there are some drawbacks with regards to aluminium alloys like it results in abrasive and scratchy machined surface due to its poor wear resistance which becomes detrimental for using it in case of precise engineering output as required in making propeller blades of aircraft, in making of transmission casing used in helicopters where there is need for even lighter material. Along with this, the poor biocompatibility of aluminium when it is used in case of food packaging and cooking utensils might link to Alzheimer’s disease as stated by Christopher exley et al (2014)[1]. To solve the above mentioned problems of aluminium alloys demand for new options emerged and magnesium alloys proved to be a viable alternative.

A literature review has been undertaken in order to obtain useful information. It involves identifications and articulations of linkage between the literature and our topic of inquiry. Although the format of the reviewing literature can be altered by using different types of criteria, the purpose of the research remains static. . In recent years, Sankaran & Mishra et al (2017)[2] reviewed that the demands of Mg alloys are increasing in various different machining techniques. This can be attributed to the fact that Mg alloys can be used in case of lighter workload as it is one of the lightweight metallic materials. Even more noteworthy is that Mg alloys are 35 percent more lightly as compared to the Al alloys. Viswanathan et al. (2014)[3] aimed to optimize cutting parameters such as cutting speed, feed rate, and depth of cut while dry turning an AZ91D Mg alloy. Among the multiple factors listed above, feed rate was shown to be the most impacting parameter. Adel et al (2018)[4] built an artificial neutral network using matlab to predict surface roughness over minimal machining time at prime machining cost. The ANN model was able to predict with 1.35 percent accuracy. Dutta & Narala et al (2021)[5] successfully optimized turning parameters for newly developed AM Mg alloy using Taguchi technique. It was concluded that depth of cut bears maximum influence on cutting forces and feed has maximum influence of surface roughness. Danish et al (2019)[6] investigated the influence of cryogenic treatment while performing turning operation of AZ31C alloy in order to analyse surface integrity parameters. It concluded that cryogenic machining improves surface quality, corrosion resistance and reduces ignition risk. Rafai et al (2013)[7] found that depth of cut is not a significant factor while machining unless there is built up edges formed around the cutting tool. Eker et al (2014)[8] investigate about the machining of Mg alloy under dry and MQL conditions. It was proven that MQL is beneficial technique in reducing the cutting temperature which in turn improves tool life as well as it helps in eliminating BUE formation. Bruschi et al (2018)[9] have experimentally performed the turning operation on AZ31 alloy under three different cutting conditions i.e. dry cutting, wet cutting and cryogenic cooling. It was concluded by them that the process with cryogenic treatment results into machined surface with improved corrosion resistance. Song et al (2013)[10] stated that AZ91D Mg alloys has the potential to be the implant biomaterial as it is harmless for human being, due to the fact that magnesium alloys are biodegradable in fluid of human body and Mg+2 helps in quick growth of bone tissue . Chakraborty Banerjee et al (2019)[11] investigated various types of material to analyse about their natural biocompatibility which includes magnesium, titanium, cobalt chromium alloys as well as stainless steel. Among these materials, it was observed that magnesium alloys were found to be having best potential for biomaterial implants as it has lower corrosion rate in human blood fluid as compared to others. Dutta et al (2020)[12] explained that even nose radius has an important role in deciding machined surface quality by performing turning operation on a magnesium work specimen. The result indicated that larger the nose radius better will be the surface produced.

According to the above-mentioned literature study, the majority of researchers have undertaken optimization analysis using feed, speed, and depth of cut as likely input factors. Only a few of them have used cutting tool geometry as an input parameter, and the majority have not explored it. Similarly, the output variable has primarily been focused on surface roughness, with only a handful taking into account other variables.

Based on a comprehensive analysis of the literature, it was determined to include the aspect of cutting tool geometry in this project, and therefore, in addition to speed, feed, and depth of cut, the approach angle of the cutting tool would be one of the input parameters. We will use surface roughness, material removal rate, tool wear rate, and machining time as output parameters to examine economical machining, which is directly related to the quality of the product produced after machining.

The aim of this project is to optimise the cutting parameters in order to investigate their impact on the output variables by using various statistical tools like Taguchi analysis and ANOVA analysis and Regression modelling:

1. To investigate the impact of various cutting parameters on the surface roughness material removal rate, tool wear rate and machining time obtained after turning magnesium alloy.
2. To develop relation among the various chosen influencing parameters in order to evaluate the percentage of contribution among them in case of the surface finish, material removal rate, tool wear rate and machining time obtained after performing the turning operation.
3. To make a comment regarding the overall cost of production based on the quality of the surface finish, material removal and tool wear rates & machining time obtained by optimizing the influencing cutting parameters.  

II. METHODOLOGY

A.  Material Selection

The experiment has been performed on a single piece magnesium AZ31B alloy. The specimen was of cylindrical bar shape with diameter 20 mm and the length of the specimen was taken as 300 mm. Table 1 shows the chemical composition of the alloy.

The AZ31B alloy falls under the wrought magnesium alloy category having good room temperature strength, ductility, corrosion resistance and weld ability. Along with its utility in aircraft and medical sectors it is mostly used in making camera casing, cell phones, laptop cases, speaker cones and concrete tools.

B. Cutting Tool Selection

The magnesium AZ31B has been turned by using carbide inserts. In order to study the effect of cutting tool while machining the Mg alloy it has been decided to take the tool insert angle or approach angle as one of the input variables and for that reason three different carbide tools having angles 35?, 55?, 80? are being considered. Table 2 shows the key specification of the walter cutting tool.

The reason for selecting carbide cutting tool for turning Mg AZ31B alloy can be attributed to the fact that it gives us the assurance of safe machining environment as there is chances of ignition of Mg alloy due to overheating of the material. While machining the Mg alloy there remains a chance of buit up edge formation which can be avoided by using carbide tool and the cost of carbide tool also plays an important role as it is less expansive as compared to polycrystalline diamond tools.

C. CNC Machine specification

 The experimental work has been carried out on CNC LT-16 XL having machine number 381 using CNMG inserts having tool corner radius 0.8 mm. The CNC system used is Fanue Oi Mate-TD and the CNC package used is Beeta 8i s (feed motor- 2 Nos), Beeta 6i (spindle), with SVPM-11 i.

D. Surface roughness tester specifications

In order to analyse about the quality of the machining output of a component, one of the most important characterstic being investigated is the measurement of surface roughness. The surface roughness measurement of the 9 turned out specimens with regard to this project was done on a portable surface roughness tester named as Mitutoyo surftest SJ210 series having a model number UI312-0913.

E. Vickers Hardness Machine Specification

Magnesium alloys while machining has a tendency to get iginited which makes it a bit challenging material for machining purpose. One of the prime reason for the ignition can be stated that it results into higher cutting temperature while machining the Mg alloy. In order to reduce the chances of self ignition of the material, cryogenic soaking can be an effective method. As per Gunasekhran et al (2021)[13], cryogenic soaking of duration about 60 minutes was found to be effective in reducing the chances self iginition of the Mg AZ91D alloy. In order to check the enhenced hardness of the material vickers hardness test was performed on the Mg AZ31B alloy. Since the workpiece was smaller in length and size vickers hardness test was preferred over the brinell hardness test.

F. Experimental Design Techniques

For optimizations of the cutting parameters i.e. speed, feed, depth of cut and approach angle of cutting tool following methods are used:

1. Taguchi’s Orthogonal Array (OA): Taguchi’s OA has been used for the proper setting of the factors with their respective levels in the OA.
2. Analysis of Variance (ANOVA): It is used to test the significant parameters in design of experiments as it shows the percentage of contribution for them.
3. Signal-to-Noise (S/N) Ratio: It is used to find the optimal settings of the parameters for optimum results
4. Main Effects Plot for S/N Ratio & Means: These analyses also show the optimal settings of the parameter for optimum result. It is drawn for checking the parameter level-wise in the DOE.

In order to achieve the specific aim of the research analysis, three different criteria are available for that purpose as stated below in the following table 4:

Table 4

Available Criteria For Taguchi Analysis Using Minitab 19

SIGNAL TO NOISE RATIO	AIM OF THE EXPERIMENT	DATA CHARACTERSTICS	S/N RATIO FORMULAS
Larger the better	Maximize the response	Positive	S/N = −10 *log(Σ(1/Y2)/n)
Smaller the better	Minimize the response	Non negative with a target value of zero	S/N = −10 *log(Σ(Y2)/n))
Nominal the best	Target the response as close as possible to standard deviation	Positive, zero or negative	S/N = −10 *log(σ2)

The optimization of the response variables are done as per available criteria are as follows:

1. Surface Roughness : Lower-The-Better
2. Material Removal Rate : Higher-The-Better
3. Tool Wear Rate : Lower-The-Better
4. Machining Time : Lower-The-Better

Regression model has been used to identify the the critical parameter among the speed, feed, depth of cut and approach angle of the cutting tool. Regression modelling is basically a statistical approach that defines mathematical relationship between one or more independent variables with as many numbers of dependent variables.

In this project, we will be dealing with linear regression modelling where the dependent and independent variables are related to one another through a linear equation as stated below.

 

 

 

 

The most important table among all the tables provided after performing regression analysis is the model summary table. Some of the key elements which will feature in the model summary table are pointed out as below:

a. S: It is the deviation between fitted value and data value. Lower the value of S better will be the model however lower value of S not always provide correct scenario

b. R-Sq: It is used to explain the percentage variation of response by the model. Higher of R-Sq provides better fit to the model. Its value lies between 0 to 100%

c. R-Sq (adj): It is used to compare models that have different number of predictors. It helps in determining which of the parameters might not be helpful in improving the model and hence that can be discarded.

Another important table which needs to be explained is the Coefficient table. In this table, the column Coefficient is describing the values which are being multiplied to the respective described term in the regression equation. It represents change in the response with respect to variation in the term.

The column SE Coefficient represents the standard error of the coefficient estimates. Smaller the value of SE more precise will be the estimates.

The next column represents T-value which is the ratio of Coefficient to its standard error. It can be used to reject null hypothesis but more often P-value is used for that purpose.

The column P-value represents the probability measure that provides evidence against the null hypothesis. A P-value of less than or equal to 0.05 for a 95% CI indicates that it is statistically significant. The last column represents VIF value which represents how much multi-collinearity exists in the regression analysis. A VIF value of more than 5 represents that the regression coefficient is poorly estimated due to extreme multi-collinearity.

Contour plots are generally used to show the relation among the two input variables on an individual output parameter. Contour plots can be used to investigate desired output parameters and operating variables.

A contour plot consists of following elements:

• On the x- and y-axes, there are predictors.
• Contour lines are drawn between places with the same response value.
• Ranges of response values are shown by coloured contour bands.

III. RESULTS AND DISCUSSION

A. Taguchi Method for Optimization

The ranges of each of the input parameters which are selected on the basis of the manufacturer’s catalogue are shown in the table 5 given below:

TABLE 5

INPUT PARAMETERS AND THEIR LEVELS

SYMBOL	INPUT PARAMETERS	UNITS	LEVEL 1	LEVEL 2	LEVEL 3
v	Cutting Speed	rpm	800	1000	1200
f	Feed	mm/rev	0.2	0.3	0.4
d	Depth of Cut	mm	0.2	0.3	0.4
θ	Approach Angle	degree	35	55	80

Due to limited size of the work specimen AZ31B alloy, we opted for L9 orthogonal array design as it is more compact and will help us to perform the requisite engineering experimental design in order to achieve our goal with minimum number of experiments to be performed. The required Taguchi L9 array obtained as per above stated levels are provided below in the table 6.

TABLE 6

REQUIRED L9 ARRAY OF THE PROJECT

Run	Cutting Speed (rpm)	Feed (mm/rev)	Depth of Cut (mm)	Approach Angle (?)
1	800	0.2	0.2	35
2	800	0.3	0.3	55
3	800	0.4	0.4	80
4	1000	0.2	0.3	80
5	1000	0.3	0.4	35
6	1000	0.4	0.2	55
7	1200	0.2	0.4	55
8	1200	0.3	0.2	80
9	1200	0.4	0.3	35

1. Analysis of Surface Roughness

The quality of the machined component plays an important role in deciding the outcome of the machining process. The most prominent parameter in deciding this aspect is the surface roughness. Lower the value of surface roughness better will be the surface finish and the machining output will be satisfactory.

As we know that lower surface roughness is desirable so while analysing the surface roughness using MINITAB19 software we choose the lower-the-better for its optimization. The experimental values of surface roughness and S/N ratios are listed below in the table 7.

TABLE 7

EXPERIMENTAL VALUES OF SURFACE ROUGHNESS AND S/N RATIOS

Run	Cutting Speed (rpm)	Feed (mm/rev)	Depth of Cut (mm)	Approach Angle (?)	Surface Roughness (µm)	S/ N Ratio (dB)
1	800	0.2	0.2	35	5.084	-14.1241
2	800	0.3	0.3	55	7.290	-17.2546
3	800	0.4	0.4	80	3.448	-10.7513
4	1000	0.2	0.3	80	1.801	-5.1103
5	1000	0.3	0.4	35	7.729	-17.7625
6	1000	0.4	0.2	55	12.335	-21.8228
7	1200	0.2	0.4	55	3.353	-10.5087
8	1200	0.3	0.2	80	2.833	-9.0449
9	1200	0.4	0.3	35	15.037	-23.5432

For analysing and optimizing the surface roughness, the response table for S/N ratio plays an important role in deciding the levels of the input parameters that must be selected which will give us the desired lower-the-better criteria for analysis. The response table has been provided below in the table 8.

TABLE 8

 RESPONSE TABLE FOR S/N RATIOS OF SURFACE ROUGHNESS

LEVEL	CUTTING SPEED	FEED	DEPTH OF CUT	APPROACH ANGLE
1	-14.043	-9.914	-14.997	-18.477
2	-14.899	-14.687	-15.303	-16.529
3	-14.366	-18.706	-13.007	-8.302
DELTA	0.855	8.791	2.295	10.174
RANK	4	2	3	1

From the response table we can clearly observe that delta value for approach angle is highest among others thus indicating that approach angle of the cutting tool has higher influence on surface roughness as compared to other input parameters.

This response table for S/N ratios has been appropriately supported by main effects plot for S/N ratio and main effects plot for means. This plots along with the response table helps in determining the required levels for input parameters. The main effects plots for S/N ratios and means are shown in figures below.

We can see from the main effects plot for the S/N ratio that the SN value for cutting speed is highest at level-1, then falls as cutting speed is increased to level-2, then increases again at level-3, but the highest value of SN ratio remains at level-1. In comparison to cutting speed, the feed has a much simpler trend, with the largest SN value at level-1 and dropping as the feed value increases. The figure for depth of cut follows a similar pattern to that of cutting speed, in that the SN value declines as depth increase from level-1 to level-2, but then rises to its highest value at level-3. The SN plot for approach angle is much steeper than the others, indicating that it has the most influence on the response variable, with a pattern of increasing SN value as approach angle climbs from level-1 to level-3.

The increase in approach angle resulting into maximum impact on surface roughness can be attributed to the fact that icrese in approach angle gives increment in tool-workpiece contact along the direction of cutting edge and this increase in contact length results in higher surface roughness[14].

For analysis, we must choose the S/N ratio that is highest among the others for a particular level of an input parameter, or we must choose the S/N ratio that is closest to zero (0) value. We can see from the above plots and response table that level-1 for cutting speed, level-1 for feed, level-3 for depth of cut, and level-3 for approach angle must all be chosen to achieve the optimal result. Thus, using the Taguchi approach, the anticipated combination for optimum surface roughness value is v1-f1-d3-θ3.

In order to check the contribution of each the input parameters in the analysis of surface roughness, ANOVA analysis has been performed. The result of the ANOVA analysis for surface roughness is listed in table 9 provided below.

TABLE 9

ANOVA FOR SURFACE ROUGHNESS

Source	DF	SS	MS	% Contribution
Cutting Speed	2	1.119	0.5596	0.3709
Feed	2	116.219	58.1093	38.5282
Depth of Cut	2	9.320	4.6602	3.0897
Approach Angle	2	174.988	87.4941	58.0110
Total	8	301.646		100

From the above ANOVA table we can conclude that approach angle of the cutting tool has the most influence on surface roughness with 58.01% contribution followed by feed with 38.53% contribution. The depth of cut and cutting speed has the minimum influence on surface roughness with 3.09% and 0.37% contribution respectively. The pie chart given below represents percentage of contribution of the various input parameters involved.

2. Analysis of Material Removal Rate

As the machining operation deals with removal of excess material from the work specimen, in this regard material removal rate becomes an important aspect of the machining outcome. The material removal rate in case of cutting operation is desired to be higher which is in contrast with the finishing operation. So to analyse the material removal rate using taguchi method we have to choose larger-the-better criteria while dealing with the S/N ratio values.

For evaluating material removal rate in this project, we will be using the equation as stated below. The density of the workpiece AZ31B alloy has been taken as 1.77 g/cm3.

By using the above stated values and through taguchi method analysis the experimental value of MRR and S/N ratios are obtained and listed in the table 11 below.

For analysing and optimizing the material removal rate, the response table for S/N ratio plays an important role in deciding the levels of the input parameters that must be selected which will give us the desired criteria for analysis. The response table has been provided below in the table 12.

From the response table we have found that delta value for depth of cut is highest among others thus indicating that depth of cut has higher influence on material removal rate as compared to other input parameters.

This response table for S/N ratios has been appropriately supported by main effects plot for S/N ratio and main effects plot for means. This plots along with the response table helps in determining the required levels for input parameters for optimal values. The main effects plots for S/N ratios and means are shown in figures below.

We can see from the main effects plot of S/N ratios that the plot for cutting speed follows an increasing trend as SN values increase all the way from level-1 to level-3. The same tendency can be seen in the plot for feed when its SN values are increased with each level increment from 1 to 3. However, the approach angle plot differs from the others in that the SN value drops as the angle changes from level-1 to level-2 and achieves its maximum value at level-3. The curve for depth of cut is steeper than the others, indicating that it has a greater influence on material removal rate.

This higher material removal rate corresponding to higher depth of cut can be explained from the theoretical background that material removal rate is a function of depth of cut, speed and feed. As a result, a significant depth of cut leads to a high MRR, which boosts productivity and makes machining more cost-effective[15].

For analysis, we must choose the S/N ratio that is the largest among the others for a given level of an input parameter, or we must choose the S/N ratio that is not zero (0). We can plainly see from the above plots and response table that level-3 for cutting speed, level-3 for feed, level-3 for depth of cut, and level-3 for approach angle must be chosen in order to meet our goal of maximising the material removal rate and getting an optimal value. Thus, using the Taguchi approach, the anticipated combination for optimum material removal rate value is v3-f3-d3-θ3.

In order to check the contribution of each the input parameters in the analysis of material removal rate, ANOVA analysis has been performed. The result of the ANOVA analysis for material removal rate is listed in the table 13 given below.

TABLE 13

ANOVA FOR MATERIAL REMOVAL RATE

Source	DF	SS	MS	% Contribution
Cutting Speed	2	16.7888	8.3944	21.9441
Feed	2	10.0947	5.0474	13.1950
Depth of Cut	2	47.3630	23.6815	61.9096
Approach Angle	2	2.2568	1.1284	2.9499
Total	8	76.5034		100

From the above ANOVA table we can conclude that depth of cut has the most influence on material removal rate with 61.91% contribution followed by cutting speed with 21.94% contribution. The Feed has 13.2% contribution on the material removal rate and approach angle of the cutting tool has least impact with 2.95% contribution on the material removal rate. The pie chart given below represents percentage of contribution of the various input parameters involved.

3. Analysis of Tool Wear Rate

In order to achieve economical machining tool wear rate is an important parameter in this regard. Higher tool wear rate is somewhat a spoilsport in case of economical machining as it will make the cutting tool to get wear out quickly and hence there will be a need for frequent change of the cutting tool which will lead to slower production rate and ultimately it result into loss for the manufacturing organization.

Hence while analysing tool wear rate using taguchi method we will choose lower-the-better criteria while performing the requisite optimization technique.

For evaluating tool wear rate in this project, we will be using the equation as stated below. The density of the carbide cutting tool material has been taken as 15.63 g/cm3.

The difference in weight of the cutting tool before and after the experiment along with the machining time for nine different combinations of experiments is shown in the table 14 below.

By using the above stated values and through taguchi method analysis the experimental values of TWR and S/N ratios are listed in the table below.

For analysing and optimizing the tool wear rate, the response table for S/N ratio plays an important role in deciding the levels of the input parameters that must be selected which will give us the desired criteria for analysis. The response table has been provided below in the table 16.

From the response table we can conclude that delta value for depth of cut is highest as compared to others thus indicating that depth of cut has higher influence on tool wear rate among the other input parameters.

This response table for S/N ratios has been appropriately supported by main effects plot for S/N ratio and main effects plot for means. This plots along with the response table helps in determining the required levels for input parameters for optimal values. The main effects plots for S/N ratios and means are shown in figures below.

When cutting speed changes from level-1 to level-3, the main effects plot for S/N ratios of tool wear rate shows that the plot for cutting speed follows a declining trend as the SN value decreases. Since the SN value decreases significantly from level-1 to level-2, the feed plot differs from the cutting speed plot. When moving from level 2 to level 3, the SN value for feed drops dramatically. When the angle changes from level-1 to level-3, the plot for the approach angle follows the same decreasing trend of SN value. When the depth changes from level-1 to level-3, the plot for depth of cut is substantially steeper than others, with a decreasing trend.

The decrease in tool wear rate at higher value of depth of cut can be attributed to the fact that the uncoated carbide tool used in this project has good toughness and high hardness properties[16].

For analysis, we must choose the S/N ratio that is highest among the others for a particular level of an input parameter, or we must choose the S/N ratio that is closest to zero (0) value. We can plainly see from the above plots and response table that level-1 for cutting speed, level-1 for feed, level-1 for depth of cut, and level-1 for approach angle must be chosen in order to fulfil our goal of lowering the tool wear rate to an optimal value. As a result, using the Taguchi approach, the anticipated combination for optimum tool wear rate value is as follows: v1-f1-d1-θ1.

In order to check the contribution of each the input parameters in the analysis of tool wear rate, ANOVA analysis has been performed. The result of the ANOVA analysis for tool wear rate is listed in the table given below.

From the above ANOVA table we can conclude that depth of cut has the most influence on tool wear rate with 60.53% contribution followed by feed with 19.61% contribution. The cutting speed has 13.37% contribution on the tool wear rate and approach angle of the cutting tool has the least impact with 6.49% contribution on the tool wear rate. The pie chart given below represents percentage of contribution of the various input parameters involved.

4. Analysis of Machining Time

From the concepts of economics of machining, it was evident that production rate is the most important parameter in achieving profits for the manufacturing organization. Slower production rate results in loss of revenue generation as the requisite number of components cannot be produced to meet the demand of the consumers. With respect to production rate, machining time required for each component becomes a vital cog in determining optimum production rate for the organization which will ultimately turn it into a profitable venture.

As we know that lower machining time is desirable so while analysing the machining time using MINITAB19 software we choose the lower-the-better for its optimization.

The various signal to noise ratio values has been recorded. The experimental values of machining time and S/N ratios are listed below in the table 18.

For analysing and optimizing the machining time, the response table for S/N ratio plays an important role in deciding the levels of the input parameters that must be selected which will give us the desired criteria for analysis. The response table has been provided below in the table 19.

From the response table we can conclude that delta value for depth of cut is highest as compared to others thus indicating that depth of cut has higher influence on machining time among the other input parameters.

This response table for S/N ratios has been appropriately supported by main effects plot for S/N ratio and main effects plot for means. This plots along with the response table helps in determining the required levels for input parameters for optimal values. The main effects plots for S/N ratios and means are shown in figures below.

From the main effects plot it can be observe that the plot for cutting speed is following an increasing trend with SN value increases when speed increases from level-1 to level-3. The plot for feed also follows the same increasing trend for SN value when feed changes from level-1 to level-3. The plot of approach angle is different as compared to others as the SN value decreases when angle changes from level-1to level-2 and again rises to attain the value at level-3. The plot is steeper for depth of cut compared to others suggesting it has the maximum influence on machining time.

The higher depth of cut resulting into lower machining time can be explained by the theoretical concept that high depth results into high material removal rate which enables to remove maximum material from the workpiece thus  increases the rate of production which in suggests reduced processing or machining time[15].

For analysis purpose we must choose that S/N ratio for a given level of an input parameter which is highest among the others or we have to select that S/N ratio which closer to zero (0) value. From the above plots and response table we can clearly observe that level-3 for cutting speed, level-3 for feed, level-3 for depth of cut and level-1 for approach angle must be selected in order to achieve our objective of lowering the machining time for obtaining an optimal value of it. Thus the predicted combination for optimum machining time value using Taguchi method can be represented as v3-f3-d3-θ1.

In order to check the contribution of each the input parameters in the analysis of machining time, ANOVA analysis has been performed. The result of the ANOVA analysis for machining time is listed in the table given below.

TABLE 20

ANOVA FOR MACHINING TIME

Source	DF	SS	MS	% Contribution
Cutting Speed	2	10.7065	5.3532	21.7886
Feed	2	11.3635	5.6817	23.1257
Depth of Cut	2	26.3371	13.1685	53.5983
Approach Angle	2	0.7308	0.3654	1.4872
Total	8	49.1379		100

From the above ANOVA table we can conclude that depth of cut has the most influence on machining time with 53.6% contribution followed by feed with 23.12% contribution. The cutting speed has 21.79% contribution on the machining time and approach angle of the cutting tool has the least impact with 1.49% contribution on the machining time. The pie chart given below represents percentage of contribution of the various input parameters involved.

5. Prediction and Confirmatory Test Analysis

After obtaining the optimum levels of the input parameters i.e. cutting speed, feed, depth of cut and approach angle we can use them in predicting the optimal value for each of the concerned output i.e. surface roughness, material removal rate, tool wear rate and machining time.

These predicted optimum values of the concerned outputs are done by using the equation as stated below[17]

In table 21 we are enlisting the predicted optimum values of the outputs i.e. surface roughness, feed, depth of cut, approach angle as well their corresponding optimum S/N ratio value.

TABLE 21

PREDICTED OPTIMUM VALUES OF THE OUTPUT PARAMETERS AND CORRESPONDING S/N RATIOS

Output Parameters	Optimum Levels	Predicted Values	Predicted S/N ratio
Surface Roughness	v1-f1-d3-θ3	3.475 µm	-1.96 dB
Material Removal Rate	v3-f3-d3-θ3	4183.33 mm3/min	73.74 dB
Tool Wear Rate	v1-f1-d1-θ1	1.753 mm3/min	-4.85 dB
Machining Time	v3-f3-d3-θ1	0.516 min	3.45 dB

 

 

 

 

 

 

 

 

In order to compare this predicted value, we need to select an initial level for all the input parameters along with which the comparison will be made. Hence we decided to select level-2 as initial level for all the input parameters and evaluate the predicted values of all the output parameters at this level. 

TABLE 22

COMPARISONS BETWEEN PREDICTED VALUES OF INITIAL LEVEL AND OPTIMUM LEVEL

Output Parameters	Initial input level	Predict-ed value of output	Predicted S/N Ratio	Predicted optimum level	Predicted  optimum value of output	Predicted optimum S/N Ratio	Improve-ment achieved or Not
Surface Roughness (µm)	v2-f2-d2-θ2	9.304	-18.78	v1-f1-d3-θ3	3.475	-1.96	Yes
Material Removal Rate (mm3/min)	v2-f2-d2-θ2	2287.4	67.61	v3-f3-d3-θ3	4183.33	73.74	Yes
Tool Wear Rate (mm3/min)	v2-f2-d2-θ2	2.46	-8.93	v1-f1-d1-θ1	1.753	-4.85	Yes
Machining Time (min)	v2-f2-d2-θ2	1.13	-1.39	v3-f3-d3-θ1	0.516	3.45	Yes

The final step involved in any of the engineering experimental design project is to perform a confirmatory test with an aim of checking if there is any significant difference in the predicted optimum value of the outputs and the experimentally obtained value of the outputs by conducting experiments at the prescribed optimum level of the input parameters.

TABLE 23

CONFIRMATION TEST RESULTS OF ALL THE OUTPUT PARAMETERS

Output Parameters	Initial level values	Predicted optimum level values	Experimental values at optimum level	Difference between predicted & experimental values	% reduction/ expansion obtained w.r.t initial level
Surface Roughness (µm)	9.304	3.475	4.187	0.712	54.98
Material Removal Rate (mm3/min)	2287.4	4183.33	3967.69	215.64	73.46
Tool Wear Rate (mm3/min)	2.46	1.753	1.839	0.086	25.24
Machining Time (min)	1.13	0.516	0.783	0.267	30.71

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Thus from the above confirmation result table, we can conclude that taguchi method used for optimization of these cutting parameters has helped in improving machinability of the work specimen AZ31B used in this project. With desired improvement in these critical output parameters has helped us in achieving the objective of economical machining of the work specimen used.

The trend obtained in the improvement of output parameters is similar to the results obtained by P.Siviah et al (2019)[18] while machining 17-4 PH stainless steel having surface roughness and flank tool wear as the output parameters.

B. Regression Modelling

1. Regression Analysis of Surface Roughness

In order to fit a linear regression equation, it must satisfy the assumption that all the concerned roughness data are having normal distribution. Hence normality test must be performed and it is indicated by plotting a probability plot for the given data and the P-value for probability plot must be more than 0.05 in order pass the normality test.

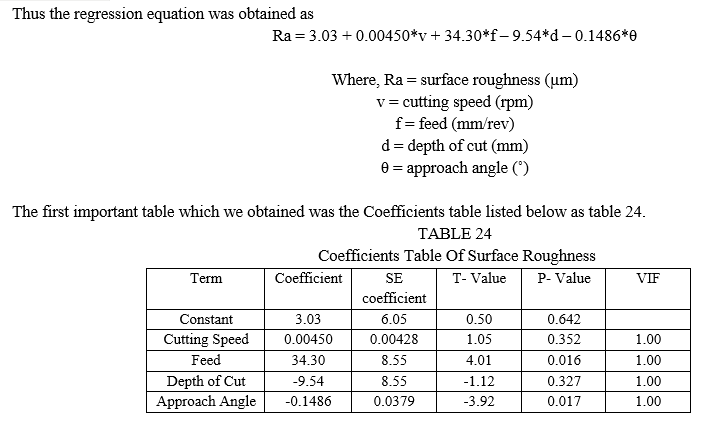
Thus we can conclude that that feed has the maximum influence on the surface roughness having a P-value of 0.016 which is closely followed by approach angle of the cutting tool as the second most influencing parameter with a P-value of 0.017. All the input parameters have a VIF value of 1.00 which shows that the regression coefficients are not correlated among themselves.

The next important table which we obtain as a part of the regression analysis is model summary table. The table 25 listed below represents the model summary.

From the above table, it can be concluded that the regression model for surface roughness has a R2 value of 89.41 % which suggests that the regression fit between surface roughness and the input parameters is a satisfactory one.

The next important table which we obtain was that of ANOVA analysis. It helps in determining the percentage of contribution of the input parameters in case of this regression model.

From the above table we can conclude that Feed has maximum influence on surface roughness with 47.63 % and is closely followed by approach angle of cutting tool with 45.41%. The cutting speed and depth of cut has a minimal contribution of 3.28 % and 3.68 % respectively.

The above results can also be described by using a pareto chart for standardized effect with surface roughness being the response. The figure is given below.

The last outcome which we obtain after performing a regression analysis was residual plots for surface roughness. This is a combination of four plots namely histogram, normal probability plot, versus fits and versus order. The residual plots for surface roughness are shown in the figure below.

We can observe that the histogram has no outliers and is somewhat skewed. The normal probability plot is approximately linear which means it is in consistent with a normal distribution. The residual versus fitted value shows random pattern which suggest that residual has constant variance. The residual versus observation order shows random pattern which means that the data was collected and can be used to obtain non-random error.

2. Regression Analysis of Material Removal Rate

In order to fit a linear regression equation, it must satisfy the assumption that all the concerned MRR data are having normal distribution. Hence normality test must be performed and it is indicated by plotting a probability plot.

We can conclude that that depth of cut has the maximum influence on the material removal rate having a P-value of 0.012 followed by cutting speed as the second most influencing parameter with a P-value of 0.059. The other parameters like feed and approach angle of cutting tool with P-values 0.091 and 0.925 respectively are not much significant as per regression analysis. All the input parameters have a VIF value of 1.00 which shows that the regression coefficients are not correlated among themselves.

The next important table which we obtain as a part of the regression analysis is model summary table. The table 28 listed below represents the model summary.

TABLE 28

 MODEL SUMMARY

S	R-sq	R-sq (adj)
401.555	88.43 %	76.87

From the above table, it can be concluded that the regression model for material removal rate has a R2 value of 88.43 % which suggests that the regression fit between material removal rate and the input parameters is a satisfactory one.

The next important table which we obtain was that of ANOVA analysis. It helps in determining the percentage of contribution of the input parameters in case of this regression model.

TABLE 29

ANOVA TABLE FOR REGRESSION MODEL OF MATERIAL REMOVAL RATE

Source	DF	Adj SS	Adj MS	F-value	P-value	%contribution
Cutting Speed	1	1109353	1109353	6.88	0.059	22.49
Feed	1	790417	790417	4.90	0.091	16.03
Depth of Cut	1	3030546	3030546	18.79	0.012	61.45
Approach Angle	1	1633	1633	0.01	0.925	0.033
Error	4	644985	161246
Total	8	5576934				100

 

 

 

 

 

 

 

 

 

 

 

 

From the above table we can conclude that depth of cut has maximum influence on material removal rate with 61.45 % and is followed by cutting speed with 22.49%. The feed has 16.03% contribution and approach angle of cutting tool has a miniscule contribution of 0.033%.

The above results can also be described by using a pareto chart for standardized effect with material removal rate being the response.

The last outcome which we obtain after performing a regression analysis was residual plots for material removal rate. The residual plots for material removal rate are shown in the figure below.

normal distribution. The residual versus fitted value reveals a random pattern, implying that the residual variance is constant. The residual versus observation order displays a random pattern, indicating that the data was gathered and can be used to calculate non-random error.

3. Regression Analysis of Tool Wear Rate

In order to fit a linear regression equation, it must satisfy the assumption that all the concerned TWR data are having normal distribution. Hence normality test must be performed and it is indicated by plotting a probability plot.

Along with this regression equation, the first important table which we obtained was the Coefficients table. The table has been listed below as table 30.

TABLE 30

 COEFFICIENTS TABLE OF TOOL WEAR RATE

Term	Coefficient	SE coefficient	T- Value	P- Value	VIF
Constant	-4.47	1.96	-2.28	0.085
Cutting Speed	0.00186	0.00139	1.34	0.251	1.00
Feed	5.69	2.78	2.05	0.110	1.00
Depth of Cut	12.22	2.78	4.40	0.012	1.00
Approach Angle	0.0158	0.0123	1.28	0.269	1.00

 

 

 

 

 

 

 

 

 

 

 

Thus from the  above table  we can conclude that that depth of cut has the maximum influence on the tool wear rate having a P-value of 0.012 followed by feed as the second most influencing parameter with a P-value of 0.110. All the input parameters have a VIF value of 1.00 which shows that the regression coefficients are not correlated among themselves.

The next important table which we obtain as a part of the regression analysis is model summary table. The table 31 listed below represents the model summary.

TABLE 31

MODEL SUMMARY

S	R-sq	R-sq (adj)
0.680566	87.09%	74.18%

From the above table, it can be concluded that the regression model for tool wear rate has a R2 value of 88.43 % which suggests that the regression fit between tool wear rate and the input parameters is a satisfactory one.

The next important table which we obtain was that of ANOVA analysis. It helps in determining the percentage of contribution of the input parameters in case of this regression model.

TABLE 32

ANOVA TABLE FOR REGRESSION MODEL OF TOOL WEAR RATE

Source	DF	Adj SS	Adj MS	F-value	P-value	%contribution
Cutting Speed	1	0.8348	0.8348	1.80	0.251	6.68
Feed	1	1.9426	1.9426	4.19	0.110	15.55
Depth of Cut	1	8.9573	8.9573	19.34	0.012	71.67
Approach Angle	1	0.7618	0.7618	1.64	0.269	6.1
Error	4	1.8527	0.4632
Total	8	14.3491				100

We can conclude that depth of cut has maximum influence on tool wear rate with 71.67 % and is followed by feed with 15.55%. The cutting speed has 6.68% contribution and approach angle of cutting tool has a contribution of about 6.1%.

The above results can also be described by using a pareto chart for standardized effect with tool wear rate being the response. The figure provided below showing the requisite pareto chart.

The histogram has no outliers and is slightly skewed, as seen in the image. The normal probability plot is nearly linear, indicating that it follows a normal distribution. The residual vs. fitted value shows a random pattern, indicating that the residual variance is constant. The residual versus observation order displays a random pattern, indicating that data was collected and can be used to calculate non-random error.

4. Regression Analysis of Machining Time

To fit a linear regression equation, it must meet the assumption that all of the machining time data in question have a normal distribution. As a result, a normalcy test must be carried out, which is represented by a probability plot.

With a P-value of 0.002, we may conclude that depth of cut has the greatest influence on machining time, followed by cutting speed as the second most affecting component with a P-value of 0.007. According to regression analysis, the feed has a high level of significance, with a P-value of 0.009. With a P-value of 0.399, the cutting tool approach angle has the least impact. The VIF value of 1.00 is shared by all input parameters, indicating that the regression coefficients are not correlated.

The next important table which we obtain as a part of the regression analysis is model summary table. The table 34 listed below represents the model summary.

From the above table, it can be concluded that the regression model for machining time has a R2 value of 96.41 % suggesting an excellent regression fit between the machining time and input parameters involved.

The next important table which we obtain after performing the regression analysis was that of analysis of variance also called as ANOVA table. It helps in determining the percentage of contribution of the input parameters in case of this regression model.

TABLE 35

ANOVA TABLE FOR REGRESSION MODEL OF MACHINING TIME

Source	DF	Adj SS	Adj MS	F-value	P-value	%contribution
Cutting Speed	1	0.212817	0.212817	26.00	0.007	24.18
Feed	1	0.183750	0.183750	22.45	0.009	20.88
Depth of Cut	1	0.476017	0.476017	58.15	0.002	54.11
Approach Angle	1	0.007294	0.007294	0.89	0.399	0.83
Error	4	0.032745	0.007294
Total	8	0.912622				100

We may infer from the above data that the depth of cut has the greatest influence on machining time (54.11%), followed by cutting speed (24.18%). The feed contributes 20.88 percent, while the approach angle of the cutting tool contributes only 0.83 percent.

A pareto chart for standardised effect with machining time as the response can also be used to describe the above results. The required pareto chart is shown in the diagram below.

The histogram has no outliers and is slightly skewed, as seen in the image. The normal probability plot is nearly linear, indicating that it follows a normal distribution. The residual versus fitted value reveals a random pattern, implying that the residual variance is constant. The residual versus observation order displays a random pattern, indicating that the data was gathered and can be used to calculate non-random error.

C. Contour Plot Analysis

At first, we will draw contour plots with surface roughness being the response variable and there will be combinations of two input predictors chosen from cutting speed, feed, depth of cut and approach angle of the cutting tool. The contour plots for surface roughness is shown by the figure given below.

We can see from the preceding figure (a) that for lower surface roughness, mid-range cutting speeds and low-range feed are appropriate. We can deduce from (b) that mid-range cutting speeds and depths of cut are preferable for reducing surface roughness. The conclusion reached from (c) is that in order to achieve lesser surface roughness, a higher cutting speed and approach angle must be selected. It can be seen from (d) that for decreased surface roughness, low feed values and mid depths of cut are desirable. Low feed and high approach angle values must be chosen from (e) for a lower value of surface roughness. It comes from (f) that a lower value of surface roughness corresponds to a mid-depth of cut and a larger approach angle.

Next we will discuss about the contour plots obtained for material removal rate. The contour plots for MRR is shown in the figure below.

We can see from above figure (a) that in order to achieve a high material removal rate, higher cutting speeds and feed rates are necessary. We can deduce from (b) that high cutting speeds and medium depths of cut are preferable for achieving a high material removal rate. The conclusion obtained from (c) is that in order to have a high material removal rate, a greater cutting speed and a low approach angle must be employed. It can be seen from (d) that for a high material removal rate, greater feed values and mid depths of cut are preferred. To get a high material removal rate, high feed values and low approach angles must be used from (e). It was discovered from (f) that a higher material removal rate corresponds to a middle depth of cut and a lower approach angle.

The contour plot analysis of tool wear rate is the next one under proceeding. The contour plots for TWR is shown in the figure below.

We can see from the above figure (a) that low cutting speeds and feed rates are appropriate for achieving lower tool wear rates. We can conclude from (b) that low cutting speeds and depths of cut are preferable for a reduced tool wear rate. The conclusion taken from (c) is that in order to reduce tool wear, a lower cutting speed and approach angle must be adopted. Low feed and depth of cut values are recommended for lower tool wear rates, as can be seen in (d). Low feed and approach angle values must be chosen from (e) to achieve a lower tool wear rate.

Next we will discuss about the contour plots obtained for machining time. The contour plots for machining time are shown in the figure below.

We can see from the above figure (a) that greater cutting speed and feed values are appropriate for reducing machining time. We can deduce from (b) that high cutting speeds and intermediate depths of cut are preferable for reducing machining time. The conclusion obtained from (c) is that in order to save machining time, a greater cutting speed and a lower approach angle must be employed. It can be seen from (d) that high feed rates and mid depths of cut are desired for shorter machining times. To achieve a decreased machining time, high feed rates and low approach angles must be selected from (e). From (f) it was found that lower value of machining time corresponds to mid values of depth of cut and lower values of approach angle.

D. Hardness Analysis

Since we know that cryogenic soaking improves a component's mechanical properties, we conducted an experiment to determine the component's hardness after the soaking period and compare it to the component's hardness before cryogenic soaking. Vickers hardness testing machine was used, and a load of 100g was applied to the specimen in three separate trials for roughly 10 seconds each.

Thus an improvement of about 33.73 % has been observed after soaking the Mg AZ31B alloy for about 30 minutes in this project work.

The trend obtained in the improvement of hardness before and after cryogenic soaking of the component is similar to the results obtained by Kaveh Meshinchi Asl et al (2009)[19] while performing deep cryogenic treatment of Mg AZ91 alloy.

IV. ACKNOWLEDGMENT

We are thankful to Dr N.Yuvaraj, Assistant Professor, Department of Mechanical Engineering, Delhi Technological University and Prof. Ranjit Kumar Das, Head of the Department, Department of Mechanical Engineering, Assam Engineering College for their advice and help both theoretically and practically. We would like to thank Dr Dililp Kumar Bora of Assam Engineering College and Mr Aniket Roy Choudhary, Senior CNC operator (ad-hock), MSME Tool room and training, Amingaon, Guwahati for providing necessary help in successful completion of this project work. At the end we are also thankful to entire faculty and staff of Mechanical Engineering Department, Delhi Technological University and Assam Engineering College for their valuable help and support.

Conclusion

In this study, we aimed to investigate about the critical cutting parameters involved in the machining of magnesium AZ31B alloy, which has a definite influence on the machined output product. Taguchi method for optimization and Regression modelling were thoroughly applied in order to achieve the intended goal of this project experimentally and statically. At the end following conclusions were drawn from this study: 1) By using taguchi method of optimization surface roughness has been successfully reduced by 54.98% , the enhancement in material removal rate by 73.46%, tool wear rate has been reduced by 25.24% and machining time has been reduced by 30.71% when compared with the output parameter values at initial input level. 2) From the ANOVA analysis as per taguchi method, it was found that surface roughness was significantly influenced by approach angle (58.01%), material removal rate was greatly affected by depth of cut (61.91%), tool wear rate was mostly influenced by depth of cut (60.53%), and machining time was also found to be influenced by depth of cut (53.6%). 3) Regression analysis has been performed in order to evaluate mathematical relation between the output parameters like surface roughness, material removal rate, tool wear rate, machining time and the input parameters like cutting speed, feed, depth of cut and approach angle of cutting tool. 4) The model summary concluded that regression model for surface roughness has a R2 value of 89.41 %, material removal rate with R2 value of about 88.43 %. The R2 value of regression model for tool wear rate and machining time was 87.09 % and 96.41 % respectively. 5) As per ANOVA analysis for regression model, surface roughness was heavily influenced by feed with 47.63% closely followed by approach angle of cutting tool with 45.41 %, depth of cut was found to be the most influencing parameter in case of material removal rate, tool wear rate and machining time with 61.45%, 71.67%, 54.11% respectively. 6) In order to investigate about interactions between the input parameters and its impact on the output parameter contour plots has been drawn for each of the output parameters like surface roughness, material removal rate, tool wear rate and machining time against the two input parameters combination out of the available input parameters. 7) As cryogenic soaking of the alloy specimen has been performed, an investigation has been performed to check increment in hardness of the specimen. It was found that hardness has been increased by 33.73 %.

References

[1] C. Exley, “What is the risk of aluminium as a neurotoxin?,” Expert Rev. Neurother., vol. 14, no. 6, pp. 589–591, 2014, doi: 10.1586/14737175.2014.915745. [2] M. Mia and N. R. Dhar, “Optimization of surface roughness and cutting temperature in high-pressure coolant-assisted hard turning using Taguchi method,” Int. J. Adv. Manuf. Technol., vol. 88, no. 1–4, pp. 739–753, 2017, doi: 10.1007/s00170-016-8810-2. [3] M. Kumar, “Optimization of Machining Parameters of Aluminum Alloy Using Taguchi Approach,” SSRN Electron. J., no. December, pp. 10–14, 2020, doi: 10.2139/ssrn.3554237. [4] A. T. Abbas, D. Y. Pimenov, I. N. Erdakov, M. A. Taha, M. S. Soliman, and M. M. El Rayes, “ANN surface roughness optimization of AZ61 magnesium alloy finish turning: Minimum machining times at prime machining costs,” Materials (Basel)., vol. 11, no. 5, 2018, doi: 10.3390/ma11050808. [5] S. Dutta and S. Kumar Reddy Narala, “Optimizing turning parameters in the machining of AM alloy using Taguchi methodology,” Meas. J. Int. Meas. Confed., vol. 169, p. 108340, 2021, doi: 10.1016/j.measurement.2020.108340. [6] M. Danish, T. L. Ginta, K. Habib, A. M. Abdul Rani, and B. B. Saha, “Effect of Cryogenic Cooling on the Heat Transfer during Turning of AZ31C Magnesium Alloy,” Heat Transf. Eng., vol. 40, no. 12, pp. 1023–1032, 2019, doi: 10.1080/01457632.2018.1450345. [7] N. H. Rafai, M. H. Othman, S. Hasan, and T. R. A. L. Sinnasalam, “The optimization in machining AISI 1030 using taguchi method for dry and flood cutting condition,” Appl. Mech. Mater., vol. 315, pp. 841–845, 2013, doi: 10.4028/www.scientific.net/AMM.315.841. [8] B. Eker, B. Ekici, M. Kurt, and B. Bakýr, “Sustainable machining of the magnesium alloy materials in the CNC lathe machine and optimization of the cutting conditions,” Mechanika, vol. 20, no. 3, pp. 310–316, 2014, doi: 10.5755/j01.mech.20.3.4702. [9] S. Bruschi, R. Bertolini, A. Ghiotti, E. Savio, W. Guo, and R. Shivpuri, “Machining-induced surface transformations of magnesium alloys to enhance corrosion resistance in human-like environment,” CIRP Ann., vol. 67, no. 1, pp. 579–582, 2018, doi: 10.1016/j.cirp.2018.04.040. [10] Y. W. Song, D. Y. Shan, and E. H. Han, “Electrodeposition of hydroxyapatite coating on AZ91D magnesium alloy for biomaterial application,” Mater. Lett., vol. 62, no. 17–18, pp. 3276–3279, 2008, doi: 10.1016/j.matlet.2008.02.048. [11] P. C. Banerjee, S. Al-Saadi, L. Choudhary, S. E. Harandi, and R. Singh, “Magnesium implants: Prospects and challenges,” Materials (Basel)., vol. 12, no. 1, pp. 1–21, 2019, doi: 10.3390/ma12010136. [12] S. Dutta and S. K. R. Narala, “Effect of tool nose radius in turning of novel Mg alloy,” Mater. Today Proc., vol. 38, no. xxxx, pp. 2675–2679, 2020, doi: 10.1016/j.matpr.2020.08.334. [13] K. Gunasekaran, G. Pradeep Kumar, R. Thanigaivelan, R. Arunachalam, and V. Shanmugam, “Optimization of Turning Parameters of Cryogenic Soaked AZ91 Magnesium Alloy using TOPSIS coupled Taguchi Technique,” J. New Mater. Electrochem. Syst., vol. 24, no. 1, pp. 49–54, 2021, doi: 10.14447/jnmes.v24i1.a09. [14] M. Boy, M. Günay, H. Demir, and ?. Çiftçi, “Effects of the Approach Angle on Cutting Force and Surface Roughness in Hard Turning of AISI 52100,” no. October 2018, 2014. [15] “What is Depth of Cut in Machining_ Its Unit, Value, Effects and Selection.” [16] M. V. Ramana, G. K. Mohana Rao, B. Sagar, R. K. Panthangi, and B. V. R. Ravi Kumar, “Optimization of surface roughness and tool wear in sustainable dry turning of Iron based Nickel A286 alloy using Taguchi’s method,” Clean. Eng. Technol., vol. 2, no. December 2020, p. 100034, 2021, doi: 10.1016/j.clet.2020.100034. [17] W. H. Yang and Y. S. Tarng, “Design optimization of cutting parameters for turning operations based on the Taguchi method,” J. Mater. Process. Technol., vol. 84, no. 1–3, pp. 122–129, 1998, doi: 10.1016/S0924-0136(98)00079-X. [18] P. Sivaiah and D. Chakradhar, “Modeling and optimization of sustainable manufacturing process in machining of 17-4 PH stainless steel,” Meas. J. Int. Meas. Confed., vol. 134, pp. 142–152, 2019, doi: 10.1016/j.measurement.2018.10.067. [19] K. M. Asl, A. Tari, and F. Khomamizadeh, “Effect of deep cryogenic treatment on microstructure, creep and wear behaviors of AZ91 magnesium alloy,” Mater. Sci. Eng. A, vol. 523, no. 1–2, pp. 27–31, 2009, doi: 10.1016/j.msea.2009.06.003.

Copyright

Copyright © 2022 Debottam Bhowmik, Susanta Kumar Kakoti. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.